DP로도 풀 수 있고, 완전탐색(DFS)로도 풀 수 있다. N이 최대 15이므로 완전탐색으로 풀어도 문제가 없다.
하지만 항상 중요한건 아이디어로,
완전탐색으로 풀 수 있는 아이디어를 얻었다면 조금만 더 시간을 쓰면 DP로도 풀 수 있을 것이다.
완전탐색(DFS)에서도 DP와 같이 주요 해결 실마리는 해당 day를 선택하지 않음 vs 선택함이다.
문제에서는 1일부터라고 나와있지만 취향따라 0부터 시작하기로 했다.

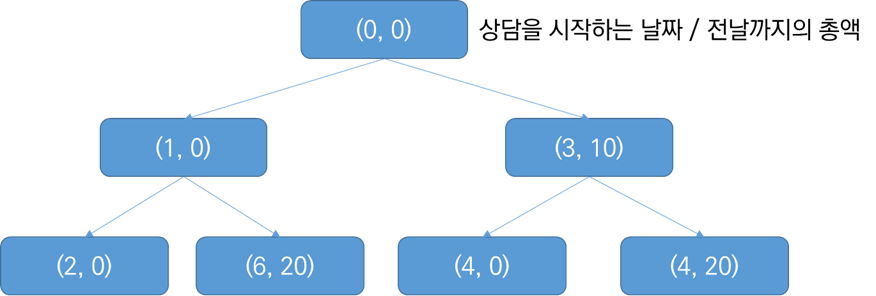
위 그래프는 DFS 트리를 그려본 것이다. (0일, 0원)에서 시작해서
왼쪽은 (0일에 일하지 않고 +1일, 여전히 0원)
오른쪽은 (0일에 일하고 +3일, 0일 상담비) 를 의미한다.
함수가 저런식으로 양쪽으로 진행된다는 것을 보여주기 위함이다.
경계값 때문에 조금 헷갈리는 문제인데, 그럴 때는 직접 대입해보자.
N이 10으로 주어졌다고 해보자. 배열은 0부터 시작하므로 마지막 상담일자는 9일이 될 것이다.
그래프 옆에 적어뒀듯이 함수 내에서 dfs(day, total) 에서 day는 상담을 시작하는 날짜이므로 기저사례에 해당하는 것은 day = N 인 경우이다. 9일이 마지막 근무일이었는데 10일에 상담을 시작할 수는 없기 때문이다.
이렇게 생각하면 마지막 근무일을 넘겼는데도 day에 10을 넣어서 dfs를 호출하는것 자체가 이상하게 보일수가 있는데, 그럴 땐 그 날을 정산하는 날짜(max_total = max(max_total, total) & return )라고 생각하자. 저 정산 과정(기저사례처리)이 필요하기 때문!
import sys
def dfs(day, total):
global max_total
# 기저 사례: 일하러 갈 수 있니?
if day >= N:
max_total = max(max_total, total) # 마지막 day는 정산하는 날
return
# 일하러 가라
dfs(day+1, total) # 선택 X
if day + T[day] <= N:
dfs(day+T[day], total+P[day]) # 선택하고 해당 일로 점프
input = sys.stdin.readline
max_total = 0
N = int(input()) # 퇴사일
T, P = [0] * N, [0] * N # T=time, P=pay (입력)
for i in range(N):
T[i], P[i] = map(int, input().split())
dfs(0, 0) # 0 ~ N일까지의 최댓값
print(max_total)
'알고리즘 > BFS와 DFS' 카테고리의 다른 글
| 17142번. 연구소 3 (0) | 2020.04.26 |
|---|---|
| 15971번. 두 로봇 (0) | 2020.04.21 |
| 16236번. 아기 상어 (0) | 2020.04.13 |
| 2178번. 미로 탐색 (0) | 2020.04.08 |
| 13460번. 구슬 탈출 2 (0) | 2019.12.31 |