신장 트리는 그래프 G=(V, E)에서 간선을 V의 갯수-1개만 남겨서 트리로 만든 것을 말한다. (V=vertex, E=edge)
최소 신장 트리(MST: Minimum Spanning Tree)는 간선들이 가중치가 있는 그래프에서 간선 가중치의 합이 가장 작은 트리를 말한다.
프림 알고리즘은 이러한 최소 신장 트리를 찾는 방법 중 하나로, 그리디 알고리즘에 속한다.
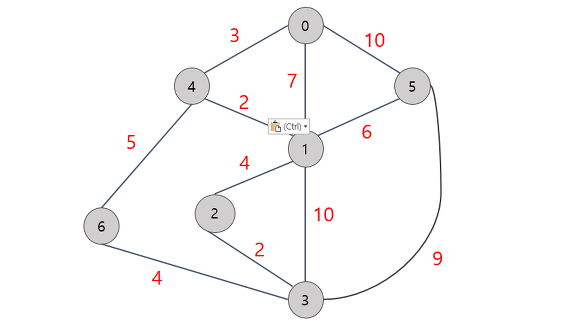
# 프림 알고리즘
INF = float('inf')
# 각 정점 사이의 가중치가 주어진다.
weight = [[0, 7, INF, INF, 3, 10, INF],
[7, 0, 4, 10, 2, 6, INF],
[INF, 4, 0, 2, INF, INF, INF],
[INF, 10, 2, 0, INF, 9, 4],
[3, 2, INF, INF, 0, INF, 5],
[10, 6, INF, 9, INF, 0, INF],
[INF, INF, INF, 4, 5, INF, 0]]
# 집합 S: 최종적으로 만들어질 트리. 처음에는 아무것도 포함되지 않았다고 가정한다.
# 프림 알고리즘에서는 모든 정점에 대해 S와의 거리를 저장한 dist라는 배열을 두고, 이 중 가장 가까운 정점을 S에 하나씩 포함시킨다.
# 새로 포함된 정점 때문에 그 정점에 인접한 점들은 S에 포함될 수 있는 최단거리가 갱신될 수 있으므로 확인 후 갱신한다.
V_NUM = len(weight[0])
dist = [INF for _ in range(V_NUM)] # 모든 정점에 대해서 집합 S와의 최단거리. 처음에는 모두 무한대라고 가정한다.
selected = [False for _ in range(V_NUM)]
dist[0] = 0 # 시작 정점을 선택하고 S에 포함하고, 거리가 0이라고 가정한다. (프림 알고리즘의 시작)
for _ in range(V_NUM): # 정점의 갯수만큼 반복
unselected = [idx for idx, val in enumerate(selected) if not val]
u = min(unselected, key=lambda x: dist[x])
# u=아직 집합 S에 포함되지 않은 정점 중에서 집합에 연결되기 위해 최소 비용이 드는 점을 구한다.
selected[u] = True
print(u) # S에 포함된 점
for v in range(V_NUM):
if weight[u][v] != INF: # u와 연결된 정점 중에서
if not selected[v] and weight[u][v] < dist[v]:
# S에 포함되지 않은 정점 중에서,
# 이미 알려진 길(dist[v])보다 더 가까운 길로 갈 수 있으면(weight[u][v]) 갱신한다. 다음에 방문하기 위해서..
dist[v] = weight[u][v]https://mattlee.tistory.com/46 를 참고하였음
'CS > 알고리즘' 카테고리의 다른 글
| Insertion Sort in Python (삽입 정렬) (1) | 2020.06.09 |
|---|---|
| 크루스칼 알고리즘 (Python) (0) | 2020.05.07 |
| Call by Value vs Call by Reference (1) | 2020.04.28 |
| Selection Sort (선택 정렬) (0) | 2020.04.24 |
| Bubble Sort (버블 정렬) (0) | 2020.04.24 |