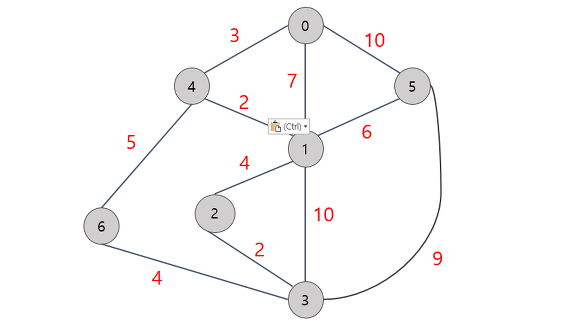
크루스칼 알고리즘은 최소 신장 트리(MST: Minimum Spanning Tree)를 찾는 알고리즘이다.
프림 알고리즘과 같이 그리디 알고리즘에 속한다.
간선을 가중치 순으로 정렬하고 가중치가 짧은 순서대로 그래프에 포함시키기 때문이다.
프림 알고리즘은 비어 있는 트리에 정점을 하나씩 추가시키면서 조금씩 트리의 크기를 키워나가는 방식이었다.
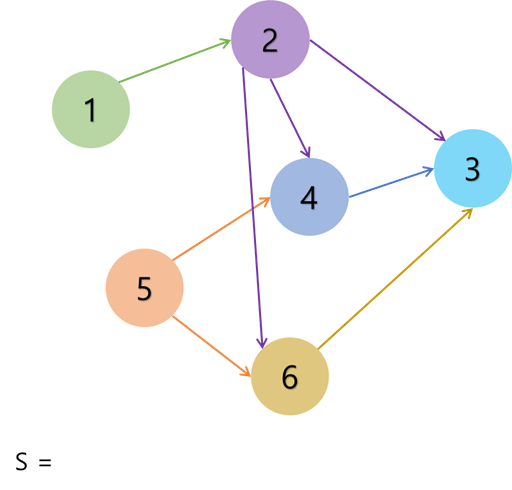
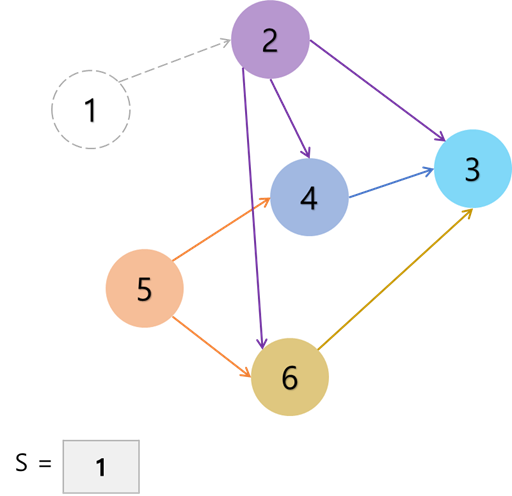
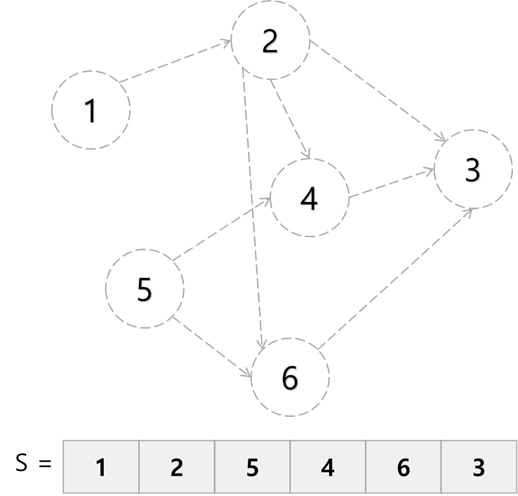
반면 크루스칼 알고리즘은 애초에 모든 정점을 크기가 1인 트리라고 가정한다.
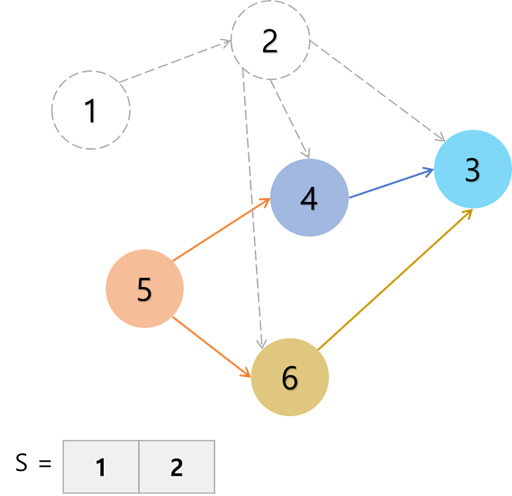
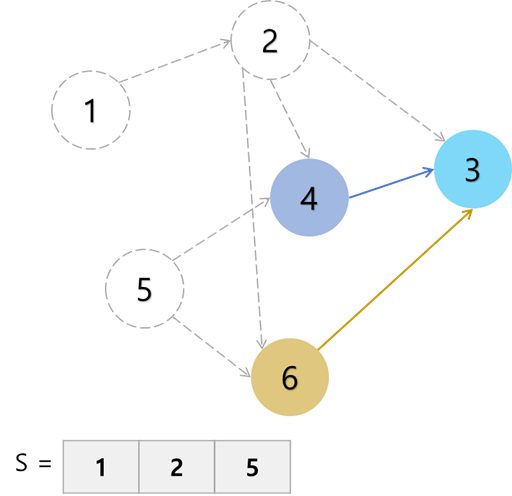
이러한 트리 사이의 간선을 가중치가 작은 순서대로 정렬한 후, 조각조각 간선을 이어 붙여서 최종적으로 하나의 트리로 만들어낸다.
이때 주의점은 정점을 이어붙이는 프림 알고리즘과는 달리 간선을 이어붙이기 때문에 가중치가 작은 순서대로 무조건 간선을 이어붙이다간 사이클이 생길 수가 있다는 것이다.
사이클이 생기면 더이상 트리가 아니기 때문에, 사이클이 생기도록 해선 안된다.
그렇다면 사이클이 생기는 지는 어떻게 알 수 있을까? 직접 노드의 부모를 타고 올라가서 루트가 같은지 확인해야 할까?
처음에는 그렇게 생각했지만, 트리마다 루트를 정해준 후에 두 트리를 합칠 때 루트를 비교하는 방법이 있다는 것을 알게 되었다.
예를 들어보자. A와 B가 결혼하려고 하는데 결혼하기 전에 혹시 A와 B의 집안이 같은 집안인지 확인하고 싶다.
그럴때 A에게 부모를 물어보고, A의 부모에게 부모를 물어보고, A의 부모의 부모에게 부모를 물어보고...계속 이것을 반복해야 할까? 너무 오래 걸리는 방법이다.
한번에 알아낼 수 있는 방법이 있다. A에게 그의 시조가 누구인지 물어보면 된다.
A의 시조는 ㅇㅇㅇ이고 B의 시조는 ㅁㅁㅁ이니까 두 집안은 다른 집안이야! 이렇게 시조를 저장해놓으면 두 집안이 같은지 O(1)만에 알아낼 수 있을 것이다.
여기 코드에서 시조, 즉 루트를 알아내는 함수는 find_set이다. find-set은 집합 처리 부분에서 나오는 그것인데 집합의 루트를 반환한다고 생각하면 된다.
그리고 두 집안이 다르면 결혼을 성사시키는데, 미국의 경우 대부분 여자가 남자의 성을 따라간다.
트리에도 이것을 적용해볼 수 있다. 남자 A의 시조가 스미스 씨였고 여자 B의 시조는 베이커 씨였는데, A와 B가 결혼함으로써 B의 시조가 스미스 씨가 되는 것이다! (실제로는 아니겠지만 크루스칼 알고리즘 사회에서는 그렇다고 치자)
즉, 노드 B의 루트가 A의 루트를 가리키게 하면 된다.
실제로 크루스칼 알고리즘에서 누가 누구를 가리킬 것이냐에 대해서는 그저 한 가지 기준을 정하면 되지만 여기서는 노드의 숫자가 큰 것이 → 작은 것을 가리키게 하는 방법을 썼다.
여기 코드에서 두 트리를 병합하는 함수는 union_set이다.
갑자기 생각난건데, 전 세계 인구를 족보 순으로 가장 가까운 순으로 연결시켜서 하나의 족보로 만든다면 그것이 크루스칼 알고리즘이 아닐까?
# 크루스칼 알고리즘
# 모든 간선의 정보를 저장할 클래스. a는 한 쪽 노드, b는 다른 한 쪽 노드이며 dist는 a와 b 사이의 가중치(거리)이다.
class Edge:
def __init__(self, a, b, dist):
self.a = a
self.b = b
self.dist = dist
# 루트 노드를 반환하는 함수.
# 루트 노드를 구할 때 그냥 root[x]해도 되겠지만 집합 처리 개념을 사용하기 위해 함수로 따로 빼냈다.
def find_set(x):
return root[x]
# 두 트리를 병합하는 함수. 일관성을 위해 노드 번호가 더 작은 것을 루트로 만든다.
def union_set(a, b):
a = find_set(a)
b = find_set(b)
if a < b:
root[b] = a
else:
root[a] = b
# edges에는 [정점 a, 정점 b, a-b 사이의 거리]를 담은 Edge 객체들이 저장되어 있다.
edges = list()
edges.append(Edge(1, 7, 12))
edges.append(Edge(1, 4, 28))
edges.append(Edge(1, 2, 67))
edges.append(Edge(1, 5, 17))
edges.append(Edge(2, 4, 24))
edges.append(Edge(2, 5, 62))
edges.append(Edge(3, 5, 20))
edges.append(Edge(3, 6, 37))
edges.append(Edge(4, 7, 13))
edges.append(Edge(5, 6, 45))
edges.append(Edge(5, 7, 73))
n = len(edges)
root = [i for i in range(n)]
# 모든 트리의 루트를 저장. 맨 처음에는 노드가 하나의 트리이므로 자기 자신이 루트이다.
total = 0 # 최단 거리
edges.sort(key=lambda x: x.dist) # 우선 간선을 가중치 순으로 정렬. 가중치가 작은 순으로 순회
for edge in edges: # 모든 간선에 대해서 반복한다.
if find_set(edge.a) != find_set(edge.b):
# 두 노드가 포함된 트리의 루트가 서로 다를 때(=두 트리를 합쳐도 사이클이 생기지 않을 때)
union_set(edge.a, edge.b) # 두 노드(가 포함되어 있는 트리)를 병합
total += edge.dist
print(total)